This is not a joke or a scam. There really is a prize of one million dollars waiting to be claimed by anyone who can solve the puzzle of placing n queens on an n×n chess-board so that no two queens threaten each other (where n is any number taken from the set of positive integers greater than three).
If you decide to take on this challenge then your program will also have to show whether an incomplete solution to the puzzle is a subset of a complete solution. For example, you will need to demonstrate whether a set of six queens placed on and 8×8 board is a subset of a solution to placing eight queens on the same board.
If you’re interested in the prize, then we’ll show you how a Python program running on a Raspberry Pi with a Sense HAT can play eight queens as a game, solve the puzzle if you get stuck, and demonstrate whether an incomplete solution is a subset of a complete solution.
Our program uses the LED matrix on a Raspberry Pi Sense HAT to represent a chessboard. The program will allow you to place and replace up to eight queens on the board in the quest to find a solution. If you get stuck with an incomplete solution, then the program will solve the puzzle for you and show you where you might have needed to move any of your queens to find a complete solution.
Don’t worry if you haven’t got a Sense HAT on your Raspberry Pi: you can also run the program in the online Sense HAT emulator – just paste the code into it.
This article first appeared in The MagPi #65 and was written by Gordon Horsington. Readers of a certain age, with good memories and an interest in the BBC Micro may remember Gordon as the author of most of the BBC Telesoftware programming tutorials broadcast on BBC 2 Ceefax during the second half of the 1980s.
Can you solve the eight queens puzzle?
Eight queens is usually played on a chessboard using eight chess pawns as surrogate queens.
Placing queens on the board at random and expecting to find a solution is not a good way to play this game. There are nearly 4.5 billion ways in which it’s possible to place eight queens on a chessboard (4 426 165 368 to be precise), but only 92 of these possibilities satisfy the requirement that no two queens can threaten each other. Although all 92 solutions appear to be unique, there are in fact only twelve truly unique solutions to the puzzle. The other 80 apparently unique solutions are transformations (rotations and reflections) of the twelve truly unique solutions. Quite clearly, we’re going to need a better strategy than just having a go.
When people play games like chess or draughts (checkers), they often use a combination of insight, cunning, and a game plan to defeat their opponent. One of the common strategies for these games is to control the middle of the board. This is quite a good way to play chess or draughts, but it’s not the way to play eight queens. Eight queens is a game played by one person and there’s no one to defeat. There has to be one queen, and only one queen, on every column and row of the board and for this reason the edges of the board can be just as important as the centre. We’re going to need a different strategy – one that’s better suited to playing eight queens.
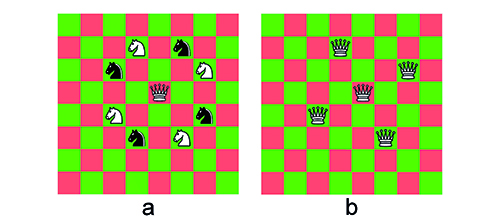
Let’s take look at chess and consider what happens when a knight threatens a queen. There are eight positions from which a knight can threaten a queen near the centre of the board (Figure 1a) and the queen cannot retaliate by removing any of the threatening knights. Don’t worry about there being eight knights on the board – we’re not playing chess, we’re just thinking about chess moves. Placing queens on a chessboard using the knight’s move to separate them can be quite a good strategy for playing eight queens. If you remove the black knights from Figure 1a and replace the four white knights with four queens, then no two queens are threatening each other (Figure 1b). We have five queens on the board and an attractive strategy. Unfortunately, as we’ll see in a moment, the five queens seen in Figure 1b are not part of a complete solution.
It doesn’t matter where you place your first queen, you can always use the knight’s move to place a second one. As we’ll soon see, this tactic doesn’t always succeed in placing all eight queens and quite often you’ll have to backtrack and move your queens around a bit before finding a solution, but it’s quite a good strategy to keep in mind. Remember, even though the knight’s move is useful, it’s not always sufficient to complete the puzzle (Figure 2.)
How can the Raspberry Pi solve the eight queens puzzle using Python and a Sense HAT?
Using the knight’s move strategy is one way in which a computer could tackle the puzzle, but it’s not the easiest nor the best one to translate into program code because it won’t find all the possible solutions. When you or I use this strategy, we tend to look at the board and the placement of the queens as a whole; we look at the empty squares as well as the queens and we use our insight into the puzzle to find a good position for our next queen. If we get stuck then we can shuffle our queens around, looking at the empty squares as well as the queens, and we can reposition the pieces taking our conceptual model of the problem into account. Insight like this is difficult to define and, without a clear definition, it’s quite challenging to model it in program code. Perhaps using a neural network might be one approach to solving this problem and maybe, one day, this puzzle could be a suitable task for a quantum computer, but for today we’ll look at how a straightforward Python program running on a Raspberry Pi can play eight queens and show us where we’re going wrong if we get stuck.
Let’s take another look at the eight queens in Figure 2. Only eight of the 64 squares are occupied by queens and most of the board is empty. There’s just one queen in every column and one queen in every row. Every solution to the eight queens puzzle has only one queen in every column and row and so we can represent the 2D chessboard in Figure 2 much more efficiently as a one-dimensional list with eight elements, rather than use a 2D list in which 56 of the 64 elements are empty. We can use the index to our eight-element list to represent the columns of the chessboard, and a number stored in each element to represent the row in which the queen is placed. The 2D LED matrix on the Sense HAT has its origin in the top left-hand corner and so the solution in Figure 2 could be represented in a one-dimensional list as [7,1,3,0,6,4,2,5]. This reduction of a 2D chessboard to a one-dimensional list is the approach we have taken in our program. Note that board columns and rows are numbered from 0 to 7, not 1 to 8. So the zeroth element in the list stores the number 7 (the queen at the bottom left), and the first element the number 1.
Finding all the possible solutions is now quite simple. All we have to do is make sure that every element of our one-dimensional list has a unique number in the range from 0 to 7 and this will ensure that the queens they represent do not threaten each other either vertically or horizontally. The queens can threaten each other diagonally and so we need to make sure that every number stored in the list does not present a diagonal threat to any other number stored in the list. This again is quite easy to check. Let’s consider the list above which has the number 3 stored in the second element. This means that neither the first nor the third element can be 2 or 4 as this would represent a diagonal challenge to the second element. Similarly neither the zeroth nor the fourth element can be either 1 or 5, and so on for every element in the list. In this way the program eliminates a diagonal challenge to the queens. This reduces the number of possible solutions from 4.5 billion to a much more manageable 92, and the Python program can find all of them very quickly. The program can also determine whether an incomplete solution on which a player gets stuck is part of a complete solution by comparing a player’s incomplete solution to all 92 possible solutions. If an incomplete solution is not a subset of a complete solution, then the program finds the closest solution to the incomplete solution and shows the player where they were going wrong.
Let’s play eight queens on the Raspberry Pi
The program runs on a Sense HAT or on an online Sense HAT emulator. All user interaction with the program is done using the Sense HAT mini joystick on a real Sense HAT, or the arrow keys and RETURN key on an emulator. In the rest of this description we’ll assume that a real Sense HAT is being used, but illustrate the puzzle with pictures from an emulator.
When the program starts, you will see a representation of a chessboard with a blue cursor (Figure 3a). You can move the cursor onto any empty square with the joystick and then press the joystick button to place a white queen over the cursor (Figure 3b). Placing queens like this is the first of three roles for the joystick button. After placing a queen, the cursor can be moved to another empty square and another queen can be placed over the cursor (Figure 3c). The program assumes that the latest move is the one you really want to make and if any queens are under threat from the latest move then the threatened queens will be removed from the board. This continues until there are eight queens on the board (Figure 3d).
Let’s suppose you get stuck and you want the computer to solve the puzzle for you. Move the cursor under any one of the queens already on the board and press the joystick button (Figure 4a). Asking for a solution in this way is the second use of the joystick button. The program will display the closest complete solution to your incomplete solution (Figure 4b). The white queens in Figure 4b represent the queens in your incomplete solution that were in the right place, the blue queens represent where your queens were in the wrong place, and the yellow queens are the ones you needed to place to complete the puzzle. If your incomplete solution is a subset of a complete solution, then there will be no blue queens on the board. If you move the cursor onto an empty square, then you can start another game.
The third and last use of the central joystick button is to exit the program. Whenever there are eight queens on the board, you can move the cursor under a queen and press the joystick button to exit the program. This is much neater than using CTRL+C on the keyboard and it keeps all the interaction with the game on the Sense HAT joystick.
# Eight Queens by Gordon Horsington
# Python 3 and Raspberry Pi Sense HAT
import sys, time, os
from sense_hat import SenseHat
sense = SenseHat()
def main():
r = [92, 0, 0]
g = [0, 92, 0]
yellow = [120, 120, 0]
blue = [0, 0, 120]
white = [120, 120, 120]
empty_board = [
g,r,g,r,g,r,g,r,
r,g,r,g,r,g,r,g,
g,r,g,r,g,r,g,r,
r,g,r,g,r,g,r,g,
g,r,g,r,g,r,g,r,
r,g,r,g,r,g,r,g,
g,r,g,r,g,r,g,r,
r,g,r,g,r,g,r,g]
results = [[0],[0],[0],[0],[0],[0],[0],[0],]
for x in range(8):
for y in range(91):
results[x].append(0)
find_all(results)
game = [-1,-1,-1,-1,-1,-1,-1,-1]
x, y, playing, display, midgame = 3, 4, True, False, False
sense.set_pixels(empty_board)
sense.set_pixel(x, y, blue)
while playing:
for event in sense.stick.get_events():
if event.action == 'pressed':
if event.direction == 'up':
y, midgame = increase(y)
if event.direction == 'down':
y, midgame = decrease(y)
if event.direction == 'right':
x, midgame = decrease(x)
if event.direction == 'left':
x, midgame = increase(x)
if event.direction == 'middle':
if display:
playing = False
else:
if good_move(game, x, y):
midgame = True
else:
best = find_best(game, results)
display = show_answer(game, sense, white, blue, yellow, results, best)
if midgame:
sense.set_pixels(empty_board)
sense.set_pixel(x, y, blue)
display, midgame = show_game(game, sense, white, blue)
sense.clear()
sys.exit()
def show_answer(game, sense, white, blue, yellow, results, best):
for count in range(8):
if game[count] >= 0:
sense.set_pixel(count, game[count], blue)
for count in range(8):
if results[count][best] == game[count]:
shade = white
else:
shade = yellow
sense.set_pixel(count, results[count][best], shade)
game[count] = -1
return True
def show_game(game, sense, white, blue):
count = 0
for column in range(8):
if game[column] != -1:
sense.set_pixel(column, game[column], white)
count += 1
if count == 8:
for count in range(3):
time.sleep(0.25)
for column in range(8):
sense.set_pixel(column, game[column], blue)
time.sleep(0.25)
for column in range(8):
sense.set_pixel(column, game[column], white)
for column in range(8):
game[column] = -1
return True, False
return False, False
def good_move(game, x, y):
if game[x] == y:
return False
game[x] = y
plus, minus = x + y, x - y
for column in range(8):
if column != x:
row = game[column]
if row == y or column + row == plus or column - row == minus:
game[column] = -1
return True
def find_best(game, results):
better = 0
best = 0
for count in range(92):
good = 0
for column in range(8):
if results[column][count] == game[column]:
good +=1
if good > better:
better = good
best = count
return best
def find_all(results):
answer = [0,0,0,0,0,0,0,0]
number, row, count, flag= 0, 0, 8, True
while number < 92:
if flag:
row += 1
flag = True
last = row - 1
answer[last] += 1
if row == 1:
answer[last] = count
count -= 1
if not answer[last]:
break
if answer[last] > 8:
answer[last] = 0
row -= 1
flag = False
if flag and row != 1:
flag = test(last, row, answer)
if flag and row == 8:
flag = False
for column in range(8):
results[column][number] = answer[column] - 1
number += 1
return
def test(last, row, answer):
while (last):
column = answer[last -1]
trial = answer[row -1]
if trial == column or trial == (column + row - last) or trial== (column - row + last):
return False
last -= 1
return True
def increase(square):
if square > 0:
square -= 1
else:
square = 7
return square, True
def decrease(square):
if square < 7:
square += 1
else:
square = 0
return square, True
if __name__ == '__main__':
main()